С.Д. Хайтун
ФЕНОМЕН НЕГАУССОВОСТИ СОЦИАЛЬНЫХ ЯВЛЕНИЙ
Автору этих строк удалось четверть века назад выявить то общее, что, кажется, свойственно разным социальным статистическим стационарным (не содержащим времени) распределениям, получаемым с помощью открытых шкал. Эти распределения в их массе имеют длинные хвосты, описывающиеся распределением Ципфа: чем меньше показатель a этого распределения, тем длиннее хвост[1].
После развертывания некорректных закрытых шкал в корректные открытые длиннохвостыми окажутся, по всей видимости, практически все социальные стационарные распределения. Значения параметра a, как правило, невелики, описываясь, в свою очередь, на случайной выборке социальных стационарных распределений ципфовым распределением с небольшим значением собственного a (a»1,3). Это явление мы обозначаем как феномен негаусовости социальных явлений, потому что распределения этого вида существенно отличаются от обычных гауссовых распределений, подчиняющихся центральной предельной теореме теории вероятностей.
Феномен негауссовости социальных явлений был установлен нами сначала на материале наукометрических распределений, а затем обобщен на социальные распределения вообще. Теоретический его анализ мы выполнили, отталкиваясь от работ по теории распределения Ципфа А.И.Яблонского, который в свою очередь опирался на Б.Мандельброта (B.Mandelbrtot), Н.Хомского (N.Chomsky) и Дж.А.Миллера (J.A.Miller) и др. авторов.
1. «Гауссовые» стереотипы
При описании феномена негауссовости приходится преодолевать ряд стереотипов, которые выработались в естественных науках у ученых, успешно применяющих там гауссовую математическую статистику и неоправданно переносящих ее на негауссовые явления.
Первый стереотип. Большинство ученых уверены в том, что хвосты распределений несущественны, отбрасывая из без зазрения совести. Для распределения Гаусса (нормального распределения) и других гауссовых распределений эта практика себя оправдывает, поскольку в их хвостах содержится пренебрежимо малая часть выборки. Для негауссовых распределений этот стереотип не срабатывает, так как их хвосты, медленно убывающие с ростом значений переменных, содержат существенную часть выборки, почему их отбрасывание ведет к значительным ошибкам.
Второй стереотип. Всем нам кажется, что средний доход делит людей пополам – 50% имеют зарплату выше средней, а 50% – ниже. Когда речь идет о многих других распределениях – по весу, росту и т.д., – то так оно и есть, поскольку эти распределения – гауссовые. Однако негауссовые распределения, включая распределение доходов, очень неоднородны. 10% ученых пишут около 90% всех публикаций, основная часть доходов падает на небольшую часть населения и т.д.. И потому основная масса ученых имеет публикаций меньше среднего числа публикаций на ученого, основная масса населения имеет доход меньше среднего и т.д.
Третий стереотип. Полтора столетия успешного применения гауссовой математической статистики на гауссовых генеральных совокупностях (см. определение в § 3), характерных для естественных наук, а также для социальных наук при использовании закрытых шкал, породили у исследователей и практиков (экономистов, социологов, демографов, статистиков и т.д.) интуитивно питаемую убежденность в том, что получаемые ими результаты не зависят от объема выборки, изменяясь от выборки к выборке только случайно. При вычислении среднего, дисперсии и других моментов распределения никто не оглядывается сегодня на объем выборки, который фигурирует только при оценке случайной ошибки выборочного значения данной величины.
При работе с длиннохвостыми (негауссовыми) распределениями этот стереотип подводит самым серьезным образом, потому что на негауссовых генеральных совокупностях моменты растут с объемом выборки. Поскольку в разных расчетах объемы выборок берутся разными, постольку при использовании моментов не просто результаты «гуляют», не выказывая должной воспроизводимости, но и вносится систематическая ошибка. Скажем, при совпадении формы распределения жителей данного города по доходам с формой такого распределения для всей страны расчетный средний доход жителя страны оказывается бóльшим среднего дохода горожанина. Этот эффект имеет чисто математическую природу, не означая, что город беднее страны в целом, медианные значения доходов для города и страны окажутся равными. Трудно представить, сколько неверных выводов было сделано экономистами и политиками, пропитанными стереотипом, о котором мы здесь говорим.
Четвертый стереотип. В социальных науках встречаются самые разные аппроксимации эмпирических распределений. При этом господствует убеждение, что никакие критерии проверки статистических гипотез о форме распределения в принципе не позволяют остановиться на какой-то одной аппроксимации. Это не совсем так, в хаосе аппроксимаций может быть наведен определенный порядок.
А именно, если на данной генеральной совокупности среднее и дисперсия зависят от объема выборки, то эта совокупность является негауссовой, а гауссовые аппроксимации на ней некорректны, корректны лишь негауссовые. Последние же все поголовно в области больших значений переменной имеют форму распределения Ципфа, порукой чему служит предельная теорема Гнеденко-Дёблина (см. § 2). Если же на негауссовой генеральной совокупности все же используется гауссовая аппроксимация, то ее выборочные параметры направленно изменяются с ростом объема выборки.
Таким образом, выбирая аппроксимацию эмпирического распределения, в общем случае следует думать обо всей генеральной совокупности, а не только о том, чтобы выбранная нами кривая легла максимально близко от эмпирических точек данной выборки из этой совокупности. Работая с данной выборкой, следует принимать во внимание всю генеральную совокупность – такова новая статистическая идеология, к которой, представляется, нам всем предстоит перейти.
2. Гауссовые/негауссовые вероятностные распределения
Следует различать вероятностные и статистические распределения. Первые – это теоретические распределения, дискретные или непрерывные. Вторые – это эмпирические распределения, они всегда дискретны и строятся на конечных выборках из генеральных совокупностей. Вероятностные распределения обслуживаются теорией вероятностей, в которой отсутствует представление о выборках и генеральных совокупностях, статистические – математической статистикой, в которой распределение предполагается выборочным. В теории вероятностей фигурируют вероятности событий, в математической статистике – выборочные частоты значений переменных. От статистического распределения можно перейти к вероятностному, устремив объем выборки к бесконечности. В этом разделе мы говорим о вероятностных распределениях, в следующем – о статистических.
В основании современной теории вероятностей лежат предельные теоремы о сходимости распределений сумм одинаково распределенных случайных независимых величин к так называемым устойчивым распределениям. Устойчивыми называются распределения, свертка которых с такими же распределениями приводит распределениям того же вида. Свертка двух распределений – это распределение суммы случайных величин, описываемых свертываемыми распределениями.
Распределения, сходящиеся у устойчивым, мы делим на два класса – гауссовые и негауссовые. Первые подчиняются центральной предельной теореме, вторые – предельной теореме Гнеденко‑Дёблина. Гауссовые распределения – это распределения, сходящиеся в указанном смысле к нормальному распределению. Гауссовые распределения никак не ограничиваются центральной предельной теоремой по своей форме. Зато она говорит, что гауссовые распределения имеют конечные первые два момента – среднее, или математическое ожидание, и дисперсию.
Негауссовые
распределения – это распределения, не сходящиеся в указанном смысле к
распределению Гаусса, но сходящиеся к другим устойчивым распределениям. Предельная
теорема Гнеденко-Дёблина ничего не говорит об этих других устойчивых распределениях,
однако накладывает ограничения на форму
негауссовых распределений: асимптотика негауссового распределения, говорит
теорема, совпадает, с точностью до медленно меняющейся функции, с
распределением Ципфа[2].
Для вероятностных негауссовых распределений ![]() , для гауссовых –
, для гауссовых – ![]() .
.
3. Гауссовые/негауссовые генеральные совокупности
Для вероятностных распределений критерием их гауссовости/негауссовости служит конечность/бесконечность дисперсии (см. § 2). Однако вероятностное распределение – это математическая абстракция, отвечающая бесконечной генеральной совокупности. Эмпирические (статистические) распределения строятся всегда на конечных выборках из генеральных совокупностей. Понятно, что моменты на таких конечных выборках из генеральных совокупностей конечны. В этой ситуации мы предлагаем от дихотомии гауссовые/негауссовые распределения перейти к дихотомии гауссовые/негауссовые генеральные совокупности. Если на данной генеральной совокупности дисперсия существенно растет с объемом выборки, то такую совокупность будем называть негауссовой, в противном случае – гауссовой.
Раскроем смысл определения. Представим себе, что бесконечная генеральная совокупность, получаемая в результате мысленного устремления к бесконечности объема данной генеральной совокупности, описывается вероятностным распределением с бесконечным моментом (средним, дисперсией или каким-либо другим). Как поведет себя этот момент, вычисляемый на выборке, с ростом объема последней? Нетрудно понять, что, поскольку впереди его ожидает бесконечное значение, то с ростом объема выборки этот момент будет неограниченно расти.
Вот почему негауссовому вероятностному распределению, имеющему бесконечную дисперсию, отвечает генеральная совокупность с дисперсией, возрастающей с объемом выборки. И вот почему мы называем такую генеральную совокупность негауссовой. Соответственно гауссовой логично назвать генеральную совокупность, на которой выборочная дисперсия не растет с объемом выборки.
Если для
вероятностного распределения переход по гауссовости/негауссовости происходит
скачкообразно (при ![]() вероятностное
распределение негауссово, при
вероятностное
распределение негауссово, при ![]() – гауссово), то для статистического
распределения такой переход осуществляется непрерывно. Считать ли данную
генеральную совокупность гауссовой или негауссовой, зависит от требуемой
степени воспроизводимости
результатов относительно изучаемых конкретных количественных соотношений. Если
относительно этих соотношений зависимость моментов от объема выборки в данной области значений объема выборки
может считаться несущественной, т.е. не искажающей этих соотношений, то данную
генеральную совокупность следует считать гауссовой. В противном случае –
негауссовой.
– гауссово), то для статистического
распределения такой переход осуществляется непрерывно. Считать ли данную
генеральную совокупность гауссовой или негауссовой, зависит от требуемой
степени воспроизводимости
результатов относительно изучаемых конкретных количественных соотношений. Если
относительно этих соотношений зависимость моментов от объема выборки в данной области значений объема выборки
может считаться несущественной, т.е. не искажающей этих соотношений, то данную
генеральную совокупность следует считать гауссовой. В противном случае –
негауссовой.
Изучая зависимость данного момента от объема выборки, следует брать равные количества выборок разных объемов, например по одной выборке, иначе картина будет искажена. Нетрудно понять, например, что при вычислении выборочного среднего тысяча выборок объемом N=10 каждая эквивалентна одной выборке объемом N=10 000. Беря для каждого значения объема выборки одно и то же число выборок, мы будем следовать реальному положению вещей: практически ведь всегда выборка данного объема из генеральной совокупности производится в единственном экземпляре.
4. Особая роль центральной предельной теоремы и предельной теоремы Гнеденко-Дёблина
Почему из всех
предельных теорем теории вероятностей в приложениях так важны именно теоремы о
сходимости распределений к устойчивым
распределениям? Ответ на этот вопрос замыкается на критерий воспроизводимости измерения. Конкретно
речь идет о воспроизводимости формы
распределения, т.е. о воспроизводимости распределения как такового. Судя по
всему, сходимость распределений к устойчивому, пусть даже отличному от данного,
обеспечивает последнему именно устойчивость формы с ростом объема выборки.
Неслучайным представляется тот факт, что теорема Гнеденко‑Дёблина справедлива
лишь для распределений с ![]() : при
: при ![]() распределение не нормируется на единицу
и, стало быть, действительно не имеет определенной формы (параметр, нормирующий
распределение на единичную площадь, с объемом выборки неограниченно растет).
Выборочные статистики такого распределения – моменты, квантили и пр., –
определяемые формой распределения, не имеют конкретных значений. Такое
измерение в принципе невоспроизводимо. Если мы хотим обеспечить ему
воспроизводимость, то вынуждены ограничиваться предельными теоремами о
сходимости распределений к устойчивым распределениям.
распределение не нормируется на единицу
и, стало быть, действительно не имеет определенной формы (параметр, нормирующий
распределение на единичную площадь, с объемом выборки неограниченно растет).
Выборочные статистики такого распределения – моменты, квантили и пр., –
определяемые формой распределения, не имеют конкретных значений. Такое
измерение в принципе невоспроизводимо. Если мы хотим обеспечить ему
воспроизводимость, то вынуждены ограничиваться предельными теоремами о
сходимости распределений к устойчивым распределениям.
Но почему из всех предельных теорем такого рода наиболее важными оказываются именно теоремы о сходимости распределений нормированных сумм одинаково распределенных независимых случайных величин, т.е. об устойчивости распределений относительно свертки? На наш взгляд, дело в том, что такая устойчивость распределений обеспечивает переменным, на значениях которых строятся распределения, аддитивность.
В самом деле, переменная аддитивна, когда на множестве ее значений действует операция сложения. При определении сложения на множестве значений переменной эти значения мыслятся независимыми и, добавляем мы сейчас, одинаково распределенными, иначе они будут относиться к разным переменным. Переменная может быть определена формой распределения ее значений, так что распределения значений разной формы отвечают разным переменным. Чтобы оставаться в пределах множества значений данной переменной, необходимо также, чтобы распределение суммы любого числа значений переменной не зависело от этого числа. Здесь мы, правда, сталкиваемся с тем, что устойчивое распределение, к которому сходится данное, в общем случае отличается от него по форме, однако известно, что с ростом числа значений переменных в нормированной их сумме устойчивое распределение устанавливается очень быстро.
Рассматривая, казалось бы, достаточно частный случай одинаково распределенных независимых случайных величин, центральная предельная теорема и предельная теорема Гнеденко‑Дёблина оказываются выделенными из всех предельных теорем теории вероятностей, образуя в совокупности фундамент аддитивности переменных. Согласно этим двум теоремам, чтобы данная переменная была аддитивной, необходимо, чтобы распределение ее значений было гауссовым или негауссовым, третьего не дано. Это условие оказывается и достаточным, если, во-первых, переменная измерена посредством естественной шкалы, так чтобы измеряемые значения не были деформированы процедурой измерения, и если, во-вторых, результаты измерения достаточно воспроизводимы.
Суммируя, можно сказать, что, согласно этим двум предельным теоремам, множество распределений, удовлетворяющих двум критериям – воспроизводимости формы распределения и аддитивности случайной переменной, на значениях которой оно построено, – исчерпывается гауссовыми и негауссовыми распределениями. Если распределение удовлетворяет этим критериям, то оно либо является гауссовым, сходясь в указанном смысле к распределению Гаусса, либо негауссовым, описываясь в области больших значений переменной распределением Ципфа[3].
5. Негауссовость социальных явлений и эволюция
Автор этих строк поначалу утверждал, что эволюция в сторону возрастания энтропии связана с переходом от гауссовых распределений, доминирующих в природных системах, к негауссовым, преобладающим в системах социальных, что органический мир занимает в этом ряду промежуточное положение и что социальный мир эволюционирует в сторону все более творческих видов человеческой деятельности как более негауссовых.
Сегодня я готов подписаться подо всем сказанным ранее относительно социального мира, однако в отношении неорганического и органического миров должен внести коррективы. Разумеется, я с самого начала знал по литературе (и писал), что в неорганическом и органическом мирах встречаются распределения Ципфа – анионов и катионов по встречаемости в морской воде, химических элементов по встречаемости в земной коре и в нашей Метагалактике, космических тел по массе, космических же частиц по энергии и т.д., – но сегодня становится ясно, что негауссовые распределения встречаются в природе гораздо чаще, чем это думалось ранее.
Во-первых,
негауссовыми оказались распределения, описывающие распределения особей данного
вида по поверхности Земли. Негауссовы и распределения растительных видов в лесу
по биомассе (кривые доминирования разнообразия). Более того, выяснилось, что
поведение животных характеризуется распределениями, негауссовость которых не уступает
негауссовости человека. Построенные нами несколько распределений, характеризующих
поведение муравьев, оказались распределениями Ципфа со значениями ![]() , тогда как, скажем,
распределение ученых по числу публикаций описывается распределением Ципфа с
, тогда как, скажем,
распределение ученых по числу публикаций описывается распределением Ципфа с ![]() .
.
Тот факт, что мозг животных, включая насекомых, генерирует распределения, сравнимые по степени негауссовости с человеческими, впечатляет. Но это только подтверждает то, что, по-видимому, негауссовые распределения в социальной и органической сферах генерируются нейронными структурами человека и животного, точнее – отдельными нейронами, которые у человека и муравья функционируют практически одинаково.
Во-вторых, сегодня все яснее становится, что распространенность негауссовых распределений тесно связана с фрактальностью наблюдаемого мира. Негауссовость является общим свойством пространственных и непространственных фрактальных (точнее, фракталоподобных) структур. В случае пространственных фракталов речь идет о негауссовости распределений фрактальных (под)систем по размерам и расстояниям между ними[4], в случае непространственных фракталов негауссово распределены составляющие фракталы (под)системы по значениям непространственных величин, характеризующих (под)системы и «барьеры» между ними (примером непространственной фрактальной структуры, генерирующей негауссовые распределения, является нейронная сеть мозга). Поскольку же фракталы и на самом деле чрезвычайно распространены в наблюдаемом мире, постольку чрезвычайно распространены в нем и негауссовые распределения.
Если стóит чему-то удивляться, так это тому, что в наблюдаемом мире, наряду с негауссовыми, достаточно часто встречаются и гауссовые распределения, особенно в окружающей нас на Земле природной среде. Гауссовы, к примеру, распределения особей по весу, размерам и значениям многих других параметров. Судя по всему, это во многом объясняется гравитацией, которая ограничивает размеры земных объектов. В общем случае ширина распределений, т.е. степень их негауссовости, определяется не только гравитацией, но и другими взаимодействиями. Там, где эти внешние ограничения несущественны, распределение объектов оказывается негауссовым, как негауссово, например, упоминавшееся распределение космических тел по массе или земных озер по площади зеркала.
Как разъясняется в ряде наших публикаций, не являясь мерой беспорядка для реальной системы, энтропия является таковой в случае отдельно взятого распределения: чем оно шире и, следовательно, проще по форме, тем больше его энтропия. Распределения, имеющие бóльшую энтропию, более длиннохвосты, т.е. более негауссовы, отвечая большему разнообразию форм. Таким образом, эволюция в сторону все большей негауссовости явлений означает эволюцию в сторону распределений со все большей энтропией. Точнее говоря, речь может идти о том, что в ходе эволюции растет доля распределений с такой максимально большой энтропией. Другими словами, с ходом эволюции все более негауссовыми становятся генеральные совокупности распределений.
По всей видимости,
в органическом мире удельный вес ментальных факторов ниже, чем в социальном. Я
по-прежнему полагаю, что если бы для органического мира была построена
случайная выборка стационарных распределений и для каждого из них было найдено
значение параметра a негауссового распределения, то
«органическое» распределение значений a оказалось бы менее
негауссовым, чем построенное нами распределение для социального мира с ![]() . В более широком
плане, если бы для всех распределений наблюдаемого мира можно было построить
распределение значений характеризующего эти распределения показателя
распределения Ципфа a, то с ходом эволюции это распределение
становилось бы все более негауссовым, т.е. характеризовалось бы все
бóльшим значением энтропии и все меньшим значением a.
. В более широком
плане, если бы для всех распределений наблюдаемого мира можно было построить
распределение значений характеризующего эти распределения показателя
распределения Ципфа a, то с ходом эволюции это распределение
становилось бы все более негауссовым, т.е. характеризовалось бы все
бóльшим значением энтропии и все меньшим значением a.
6. Возможные приложения
Аппроксимация негауссовых совокупностей гауссовыми распределениями приводит к невоспроизводимости результатов вследствие зависимости параметров таких аппроксимаций на таких совокупностях от объема выборки. Однако на негауссовых совокупностях некорректна не только аппроксимация гауссовыми распределениями, но и вообще гауссовая математическая статистика. Поясним сказанное.
Основы современной (гауссовой) математической статистики были заложены А.Кетле, Ф.Гамильтоном, К.Пирсоном, Дж.Юлом и др. В ней главную роль играют выборочные моменты и моменты вероятностных распределений. Для гауссовых вероятностных распределений, согласно центральной предельной теореме, которой они подчиняются, моменты (точнее, первые два из них, т.е. математическое ожидание и дисперсия), конечны, что делает аппарат моментов применимым.
Для статистических распределений вопрос о применимости аппарата моментов решается не столь однозначно. Здесь следует рассматривать не гауссовые/негауссовые распределения, но гауссовые/негауссовые генеральные совокупности. Для гауссовых совокупностей рост моментов с объемом выборки несуществен, для негауссовых – существен. В первом случае аппарат моментов применим, во втором – неприменим. Если мы применяем гауссовую математическую статистику на негауссовых совокупностях, то из-за роста моментов с объемом выборки результаты оказываются невоспроизводимыми. Этот их рост не только увеличивает случайные ошибки, связанные с переходом от одной выборки к другой, но и вносит никем до сих пор не принимаемые во внимание систематические ошибки.
Чтобы сделать результаты статистического анализа негауссовых явлений, какими, в частности, является социальные явления в целом, воспроизводимыми и избавиться от систематических ошибок, здесь следует перейти от гауссовой математической статистики с ее упором на моменты к негауссовой, которая будет базироваться на других статистиках распределения, сохраняющих свое значение на негауссовых генеральных совокупностях, т.е. не зависящих на них от объема выборки.
Примером негауссовой статистики распределения является показатель a распределения Ципфа. К негауссовым статистикам распределения относятся также выборочная частота значения переменной, медиана и другие квантили, геометрическое и гармоническое средние и некоторые другие. Однако гауссовыми или негауссовыми могут быть не только статистики распределения, но и коэффициенты взаимосвязи, методы оценки параметров аппроксимаций и сами эти аппроксимации, критерии статистической достоверности и пр. Под обсуждаемым здесь углом зрения должно быть пересмотрено все наработанное математиками в области методов математической статистики. Автором проведен такого рода предварительный анализ, однако здесь требуются целенаправленные усилия профессиональных математиков.
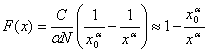 .
(С.3)
.
(С.3)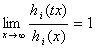 .
(С.5)
.
(С.5)