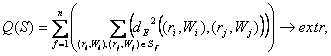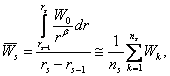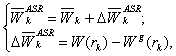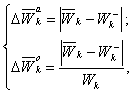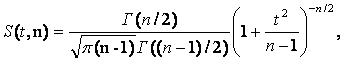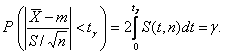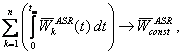// Материалы ХV конференции по философии техники и технетике и семинара по ценологии (Москва, 19 ноября 2010 г.). Вып. 47. "Ценологические исследования". – М.: Технетика, 2011. – 400 с.
ПРЕДЕЛЬНЫЙ АЛГОРИТМ НОРМИРОВАНИЯ ЭЛЕКТРОПОТРЕБЛЕНИЯ ОБЪЕКТОВ ТЕХНОЦЕНОЗА
В. И. Гнатюк, А. А. Шейнин
Основные цели и задачи в области энергосбережения определены в Указе Президента РФ от 4 июня 2008 г. № 889 "О некоторых мерах по повышению энергетической и экологической эффективности российской экономики" [1]. Для его реализации необходимы значительные инвестиции с целью замены устаревших технологий и оборудования, стабильные цены на электроэнергию, государственные экономические и административные механизмы, направленные на стимулирование заинтересованности потребителей электроэнергии в энергосбережении. Одним из важных инструментов, способствующих выполнению задач энергосбережения, является нормирование электропотребления. Разработка научно обоснованных норм и сравнение их с фактическими расходами позволяет анализировать энергоэффективность применяемых технологий, планировать мероприятия и стимулировать работу по энергосбережению, обосновывать замену старых технологий новыми. Исследование проблемы нормирования осуществляется нами с использованием техноценологического подхода [5–15].
Основоположником исследований процессов электропотребления объектов техноценологического типа и создателем научных школ по данному направлению является профессор Московского энергетического института Б. И. Кудрин. Ряд методик по нормированию электропотребления инфраструктурных объектов был разработан на кафедре электроснабжения промышленных предприятий МЭИ доцентами А. П. Пищуром и Ю. В. Матюниной, а также работающими под руководством проф. Б. В. Жилина учёными научной школы кафедры электроснабжения промышленных предприятий Новомосковского химико-технологического института. Существенный вклад в теорию нормирования электропотребления энергосистем регионов внесён учеными кафедры электроснабжения промышленных предприятий и городов Южно-Российского государственного технического университета О. А. Сухомлиновой, А. А. Сербиновской, работавшими под руководством профессоров И. И. Надтоки и А. В Седова. Также весьма большой вклад в теорию нормирования внёс профессор кафедры электроэнергетики и электроснабжения Нижегородского государственного технического университета Г. Я. Вагин [3]. Развитию методов оптимального управления электропотреблением техноценозов были посвящены многолетние исследования учёных Калининградской научной школы [5–13]. Среди наиболее ярких представителей школы следует отметить кандидатов наук С. В. Барабанова, А. Е. Северина, С. Н. Гринкевича, Д. В. Луценко, П. Ю. Дюндика и А. М. Дубовика.
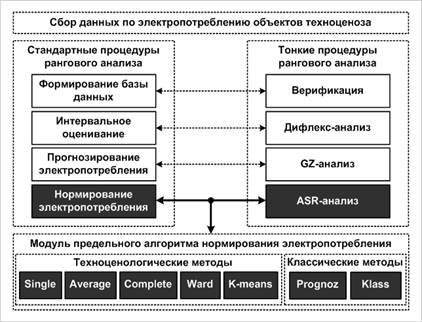
Оптимальное управление электропотреблением объектов техноценоза на системном уровне осуществляется в рамках связанной методики, включающей ряд этапов. На этапе статистического анализа осуществляется обработка данных по электропотреблению, включающая взаимосвязанные процедуры рангового анализа (формирования базы данных, интервального оценивания, прогнозирования и нормирования). С целью повышения точности расчётов стандартные процедуры рангового анализа дополняются соответствующими тонкими процедурами: верификацией базы данных, а также дифлекс-, GZ- и ASR-анализом рангового параметрического распределения [8–13]. В настоящей статье рассмотрим более подробно предельный алгоритм нормирования электропотребления как одну из форм реализации ASR-анализа – тонкой процедуры рангового анализа, существенно уточняющей нормирование (рис. 1).
В рамках техноценологического подхода нормирование – процедура оптимального управления ресурсами техноценоза, заключающаяся в определении статистических параметров (эмпирического среднего и стандарта) кластеров техноценоза, выделенных на ранговом параметрическом распределении по исследуемому функциональному параметру [13]. Классификация объектов техноценоза осуществляется методами кластерного анализа [2, 16] и позволяет выделить группы объектов, которые на определённом временнóм интервале потребляют ресурс сходным образом (рис. 2). При этом статистически внутри кластера функциональные параметры объектов должны распределяться по нормальному закону. Как показали многочисленные исследования и практическая реализация методологии, процедура нормирования в сочетании с интервальным оцениванием и прогнозированием позволяет предъявлять объектам научно обоснованные нормы расходования ресурсов (в частности – электропотребления, кВтч) [7–13].
|
Рис. 1. Стандартные и тонкие процедуры рангового анализа |
В соответствии с
[2, 3, 13, 16] кластер-процедуры реализуются на пространстве экспериментальных
данных по электропотреблению объектов в соответствии с критерием качества
разбиения на классы, который на фиксированном множестве f-разбиений ![]() на заданное число классов
на заданное число классов ![]()
|
|
(1) |
выглядит следующим образом:
|
|
(2) |
где ![]() – взвешенное
евклидово расстояние между полученными точками.
– взвешенное
евклидово расстояние между полученными точками.
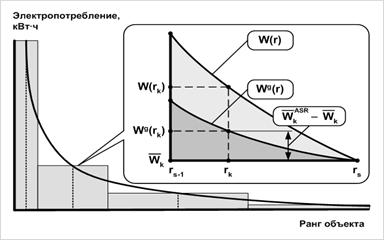
Рис. 2. Нормирование электропотребления объектов техноценоза: здесь и далее электропотребление измеряется в
кВтч за временнóй интервал (час, сутки, месяц, год и т. д.)
|
|
|
Кластер-процедура
(1) (называемая "Single" [16]) дополняется
проверкой расстояния между классами ![]() и
и ![]() , измеренного по принципу ближайшего
соседа. При этом циклично реализуется критерий:
, измеренного по принципу ближайшего
соседа. При этом циклично реализуется критерий:
|
|
(3) |
Следует отметить, что нормы могут определяться и другими методами кластерного анализа, в частности: "Average" (средней связи), "Complete" (дальнего соседа), "Ward" (Варда) и "K-means" (К-средних) [2, 3, 16]. Находят применение и классические методы: "Prognoz" (с помощью процедуры прогнозирования) и "Klass" (удельных норм) [13, 15].
Таким образом, по результатам кластер-анализа объекты техноценоза разбиваются на группы (классы, кластеры) по "сходному" электропотреблению. После этого возникает возможность определения кластерных норм электропотребления внутри каждой из групп. Кластерная норма представляет собой среднее и эмпирический стандарт, определяемые на выборке значений электропотребления рассматриваемой группы. Количество групп разбиения целесообразно иметь таким, чтобы в наиболее многочисленные из них входило не более 10–12 объектов. Среднее электропотребление для s-группы объектов определяется следующим образом:
|
|
(4) |
где ![]() –
левая и правая ранговые границы нормируемой группы объектов на распределении;
–
левая и правая ранговые границы нормируемой группы объектов на распределении; ![]() β – параметры рангового
распределения;
β – параметры рангового
распределения; ![]() – количество объектов в s-группе;
– количество объектов в s-группе; ![]() – эмпирическое значение электропотребления
k-го объекта
техноценоза
– эмпирическое значение электропотребления
k-го объекта
техноценоза
Эмпирический стандарт для этой же группы объектов:
|
|
(5) |
Процедуры кластер-анализа, будучи применены в процессе нормирования объектов техноценоза, дают неплохие результаты [9], однако обладают одним существенным недостатком. Они усредняют анализируемый параметр в пределах кластера на основе гауссовой математической статистики и тем самым не учитывают системный ресурс параметрического кластера техноценоза (см. рис. 2). Устраняется данный недостаток в рамках процедуры ASR-анализа (Adding System Resource analysis), являющейся тонким дополнением к нормированию (см. рис. 1) [13].
Реализация процедуры ASR-анализа в конечном итоге заключается в добавлении к прогнозируемому среднему нормы электропотребления объекта соответствующей его рангу индивидуальной ASR-нормы (см. рис. 2):
|
|
(6) |
где ![]() –
результирующая норма электропотребления для k-го объекта с
учётом ASR-анализа;
–
результирующая норма электропотребления для k-го объекта с
учётом ASR-анализа; ![]() –
среднекластерная норма, полученная по результатам процедуры нормирования;
–
среднекластерная норма, полученная по результатам процедуры нормирования; ![]() –
индивидуальная ASR-норма;
–
индивидуальная ASR-норма; ![]() – ранг
k-го объекта техноценоза;
– ранг
k-го объекта техноценоза; ![]() – значение
электропотребления, соответствующее на аппроксимационной кривой рангового
параметрического распределения
– значение
электропотребления, соответствующее на аппроксимационной кривой рангового
параметрического распределения ![]() k-му рангу;
k-му рангу;
![]() – гауссовое распределение в
ранговой форме, соответствующее кластерному распределению;
– гауссовое распределение в
ранговой форме, соответствующее кластерному распределению; ![]() – значение
электропотребления, соответствующее на кривой
– значение
электропотребления, соответствующее на кривой ![]() k-рангу.
k-рангу.
Приведенные на рис. 1 две группы методов нормирования формируют аппарат так называемого предельного алгоритма, что позволяет аккумулировать положительные стороны различных подходов и, как результат, повышать качество нормирования. При этом под качеством нормы понимается показатель, отражающий качество реализации процедуры нормирования по критерию близости к нижней границе переменного доверительного интервала [13]. Понятие качества нормы основывается на понимании того, что, с одной стороны, норма должна понуждать объекты к снижению ресурсопотребления, поэтому чем она ниже, тем лучше. Однако, с другой стороны, норма не может опускаться ниже величины, соответствующей значению на нижней границе переменного доверительного интервала для данного ранга (рис. 3). В противном случае выполнение нормы будет нарушать нормальный технологический процесс функционирования оборудования, установленного в данный момент на объекте. Следовательно, показатель качества нормы может быть оценен величиной абсолютного или относительного отклонения от нижней границы переменного доверительного интервала. Для оценки качества нормирования используются данные, зарезервированные в векторе верификации. Итак, количественно показатель качества нормы электропотребления может быть оценен величиной абсолютного или относительного отклонения от нижней границы переменного доверительного интервала:
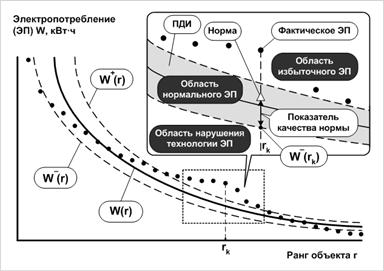
Рис. 3. К вопросу качества нормы электропотребления:
ПДИ – переменный доверительный интервал
|
|
(7) |
где ![]() –
абсолютный показатель качества нормы электропотребления k-объекта техноценоза;
–
абсолютный показатель качества нормы электропотребления k-объекта техноценоза;
![]() – относительный показатель качества
нормы;
– относительный показатель качества
нормы; ![]() – норма электропотребления;
– норма электропотребления; ![]() – эмпирическое значение
электропотребления; W(r) –
аппроксимационная кривая рангового распределения;
– эмпирическое значение
электропотребления; W(r) –
аппроксимационная кривая рангового распределения; ![]() – значение,
соответствующее k-му рангу на верхней границе переменного
доверительного интервала
– значение,
соответствующее k-му рангу на верхней границе переменного
доверительного интервала ![]() ;
; ![]() – значение электропотребления,
соответствующее k-му рангу на нижней границе
– значение электропотребления,
соответствующее k-му рангу на нижней границе ![]() .
.
Следует отметить, что выбор абсолютного или относительного показателя качества нормы зависит от специфики решаемой задачи. Если исследования осуществляются применительно к одному и тому же объекту техноценоза для сравнения результатов различных методов нормирования на отдельных этапах функционирования, то следует применять абсолютный показатель. Если нормированию подвергается выборка объектов техноценоза, то целесообразным видится относительный показатель.
При реализации процедуры ASR-анализа наиболее сложной задачей является определение соответствующей рангу каждого объекта техноценоза индивидуальной ASR-нормы, которая затем отнимается (или добавляется) от среднекластерного значения и тем самым учитывает негауссовость эмпирических выборок электропотребления. В качестве одного из эффективных методов ASR-анализа впервые предлагается так называемый предельный алгоритм нормирования, позволяющий с использованием линейной свёртки результатов нормирования отдельными методами, оптимизации вторичных норм по критерию качества, а также уточнения по ASR-отклонению получать значение предельной нормы. Как представляется, получаемая в результате реализации предельного алгоритма норма отличается от среднекластерной именно на величину ASR-нормы.
Процесс нормирования электропотребления объектов техноценоза с помощью предельного алгоритма включает следующие основные этапы (рис. 4): 1) нормирования электропотребления всеми имеющимися в распоряжении методами применительно к каждому объекту; 2) вычисления взвешенных норм; 3) реализации оптимизационного процесса с целью определения лучших вторичных норм; 4) уточнения лучших вторичных норм по ASR-отклонению; 5) получения предельных норм.
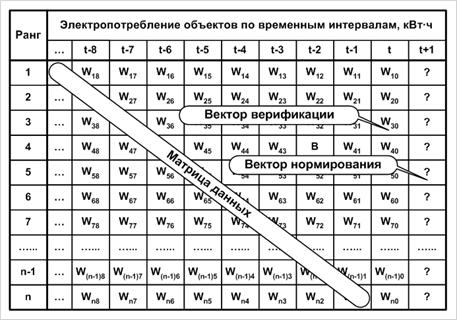
На рис. 5 приведена упрощённая структура прогнозной базы данных техноценоза по электропотреблению. Из базы предварительно осуществляется выделение ряда информационных подсистем. Фактические известные данные по электропотреблению в текущем временнóм интервале (часе, сутках, месяце, году) составляют "Вектор верификации", который выделяется из базы данных для оценки качества получаемых норм. Все остальные известные данные за прошедшие временные интервалы образуют "Матрицу данных". Нормы электропотребления на будущем временнóм интервале определяются как "Вектор нормирования". На первом этапе алгоритма осуществляется процедура интервального оценивания [7–13]. В качестве источника данных используется база данных по электропотреблению за 10–15 лет предыстории.

Рис. 4. Основные этапы предельного алгоритма нормирования.
Интервальное оценивание проводят с целью определения границ переменного доверительного интервала для вектора верификации, нижняя граница которого – гиперболическая кривая, полученная в результате аппроксимации нижних границ 95-процентных доверительных интервалов, рассчитанных для каждого из рангов рангового параметрического распределения [12, 13]. Следует ещё раз подчеркнуть, что нижняя граница переменного доверительного интервала, построенного для вектора верификации, в последующем используется для оценки качества норм, полученных на статистическом материале матрицы данных.
|
|
|
|
Рис. 5. Структура базы данных объектов по электропотреблению: Wkm – электропотребление k-го объекта техноценоза на (t–m)-временнóм интервале (час, сутки, месяц, год) |
|
Построение доверительного интервала на основе значений электропотребления рангов позволяет учесть системное влияние техноценоза и взаимное влияние объектов друг на друга. Анализ, выполненный для множества объектов различных техноценозов, позволил подтвердить предположение о нормальном распределении значений электропотребления внутри рангов, что даёт возможность на основе данных за ряд временных интервалов построить для каждого ранга доверительный интервал [12, 13].
Как известно,
если ![]() служит оценкой неизвестного параметра
служит оценкой неизвестного параметра ![]() , то доверительным называется интервал
, то доверительным называется интервал ![]() , который
покрывает неизвестный параметр с заданной надёжностью
, который
покрывает неизвестный параметр с заданной надёжностью ![]() [4]:
[4]:
|
|
(8) |
где ![]() – точность
оценки.
– точность
оценки.
Если случайная величина X распределена нормально, то по данным выборки объёмом n можно ввести случайную величину T, которая имеет распределение Стьюдента с k=n–1 степенями свободы [4]:
|
|
(9) |
где Х – выборочная средняя; m – неизвестное математическое ожидание; S – исправленное среднее квадратичное отклонение.
Плотность распределения Стьюдента определяется выражением:
|
|
(10) |
где 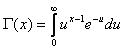 – гамма-функция (t – табличный
аргумент).
– гамма-функция (t – табличный
аргумент).
Как видно из (9), распределение Стьюдента определяется одним параметром – объёмом выборки n и не зависит от неизвестных параметров. Так как S(t, n) – чётная функция от t, то вероятность неравенства
|
|
(11) |
определяется следующим условием:
|
|
(12) |
При замене строгого неравенства в выражении (11) двойным неравенством, а также с учётом уравнения (12) получаем:
|
|
(13) |
При замене
случайных величин ![]() и S неслучайными
величинами
и S неслучайными
величинами ![]() и s, найденными по
выборке, получается доверительный интервал, покрывающий неизвестный параметр m с надёжностью
и s, найденными по
выборке, получается доверительный интервал, покрывающий неизвестный параметр m с надёжностью ![]() :
:
|
|
(14) |
где s – выборочное
среднее квадратичное отклонение; ![]() – выборочное среднее
(находится по выборке); t
– выборочное среднее
(находится по выборке); t![]() – аргумент
(находится таблично по заданным n и
– аргумент
(находится таблично по заданным n и ![]() ).
).
Данный подход для построения
доверительных интервалов имеет следующие преимущества: возможность применения
для выборок с малым объёмом (n<30), а также отсутствие неизвестных
параметров распределения. В наших исследованиях неизвестным параметром для
фиксированного ранга является истинное электропотребление ![]() , а его оценкой выступает выборочное среднее
значение электропотребления
, а его оценкой выступает выборочное среднее
значение электропотребления ![]() (рис. 6). После
аппроксимации границ переменного доверительного интервала осуществляется расчёт
взвешенных норм электро-потребления. Данная процедура реализуется путём
линейной свёртки норм, рассчитанных различными методами, включая
техноценологические, учитывающие системные свойства техноценоза и классические,
учитывающие индивидуальные особенности объектов (рис. 7).
(рис. 6). После
аппроксимации границ переменного доверительного интервала осуществляется расчёт
взвешенных норм электро-потребления. Данная процедура реализуется путём
линейной свёртки норм, рассчитанных различными методами, включая
техноценологические, учитывающие системные свойства техноценоза и классические,
учитывающие индивидуальные особенности объектов (рис. 7).
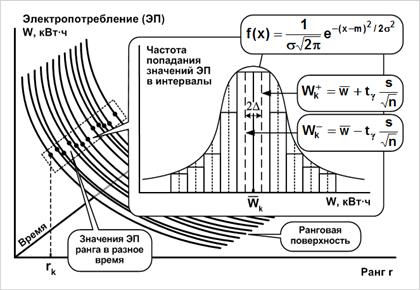
Рис. 6. Границы доверительных интервалов рангов техноценоза
Данный подход продолжает идею, реализованную нами ранее применительно к прогнозированию электропотребления в процедуре GZ-анализа [10–13]. Суть подхода заключается в следующем. На основе имеющейся базы данных по электропотреблению за определённый промежуток времени применительно к каждому объекту техноценоза реализуются все имеющиеся методы нормирования. Полученная совокупность норм оценивается по критерию близости к нижней границе переменного доверительного интервала, построенного применительно к вектору верификации, заранее выделенному из базы данных. На основе оценок норм формируется матрица весовых коэффициентов методов нормирования. При этом применяется алгоритм расчёта, реализующий принцип предпочтения: чем лучше норма, полученная данным методом, тем выше его весовой коэффициент (сумма последних для объекта равна единице). Затем применительно к каждому объекту реализуется линейная свёртка, позволяющая получить наилучшую норму электропотребления для данного объекта техноценоза на данном временнóм интервале.
Алгоритмически получению весовых коэффициентов методов нормирования предшествует расчёт отклонений значений норм от соответствующих значений на нижней границе переменного доверительного интервала.

Рис.7. Линейная свёртка методов нормирования
При этом используется абсолютный показатель качества нормирования электропотребления k-объекта техноценоза (см. выражение (7)):
|
|
(15) |
где ![]() –
норма, полученная i-м методом для k-го объекта;
–
норма, полученная i-м методом для k-го объекта; ![]() – значение электропотребления k-го
объекта на нижней границе переменного доверительного интервала.
– значение электропотребления k-го
объекта на нижней границе переменного доверительного интервала.
Это позволяет рассчитать веса i-х методов нормирования для k-го объекта техноценоза по следующим выражениям:
|
|
(16) |
В итоге для каждого объекта получаем взвешенную норму вида:
|
|
(17) |
где ![]() – вес i-го метода
нормирования для k-го объекта; q – общее количество реализуемых методов нормирования;
j –
вспомогательный формальный индекс суммирования.
– вес i-го метода
нормирования для k-го объекта; q – общее количество реализуемых методов нормирования;
j –
вспомогательный формальный индекс суммирования.
Как представляется, дальнейшее уточнение нормы может быть реализовано в процессе вторичного нормирования с последующей оптимизацией. При этом под оптимизацией норм понимается итерационный процесс определения лучшей вторичной нормы по критерию близости к нижней границе переменного доверительного интервала. Предполагается, что взвешенная норма используется при последующих расчётах как вторичная, под которой понимается норма, полученная в процессе нормирования, когда в качестве статистических данных используются не эмпирические данные по электропотреблению, а нормы, полученные на предыдущем этапе итерационного процесса. Процесс повторяется до тех пор, пока значение вторичной нормы не приблизится экстремально к нижней границе переменного доверительного интервала. Вторичная норма, которая характеризуется максимальной близостью к нижней границе переменного доверительного интервала, называется лучшей вторичной нормой (рис. 8):
|
|
(18) |
где ![]() –
лучшая вторичная норма k-ого объекта;
–
лучшая вторичная норма k-ого объекта; ![]() –
минимальная из всех вторичных норм;
–
минимальная из всех вторичных норм; ![]() – вторичная
норма k-ого объекта,
полученная на n-й итерации оптимизационного процесса;
– вторичная
норма k-ого объекта,
полученная на n-й итерации оптимизационного процесса; ![]() – значение,
соответствующее k-му рангу на нижней границе переменного
доверительного интервала.
– значение,
соответствующее k-му рангу на нижней границе переменного
доверительного интервала.
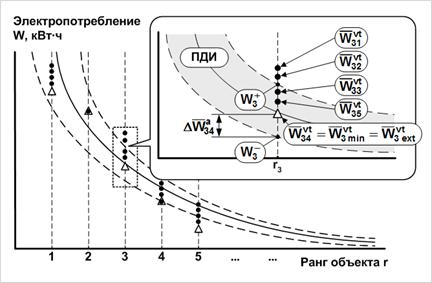
Рис. 8. К определению лучших вторичных норм
Как показали экспериментальные исследования, вторичное нормирование для разных объектов техноценоза приводит к различным результатам. Имеются пять типовых групп объектов, для которых вторичное нормирование (рис. 9): 1 – приводит к улучшению нормы до максимума, а затем – к ухудшению; 2 – к последовательному ухудшению нормы; 3 – к постоянному улучшению нормы с последующей стабилизацией данного процесса; 4 – к ухудшению до минимума, а затем – к улучшению; 5 – не приводит к улучшению нормы. Причина подобного разнообразия результатов вторичного нормирования видится в сложном согласованно-рассогласованном процессе поведения отдельных объектов по отношению к техноценозу, а также техноценоза – по отношению к объектам. Фундаментальное обоснование данного явления кроется в свойстве когерентности техноценозов [12, 13]. Процесс вторичного нормирования относится к типу безусловных задач одномерной оптимизации, которая реализуется в соответствии с критерием (18) по алгоритму, схематично показанному на рис. 10.
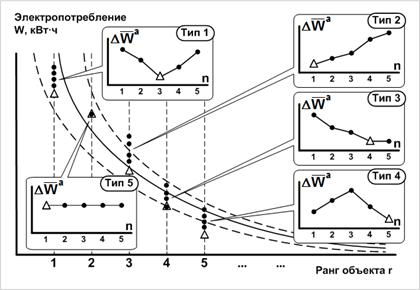
Рис. 9. Варианты результатов вторичного нормирования, осуществленного в ходе пяти итераций
Алгоритм последовательно включает два цикла, первый из которых предназначен для формирования базы вторичных норм объектов техноценоза, а второй – для фиксации лучшей вторичной нормы по каждому объекту. В первом цикле осуществляется открытый итерационный процесс, завершение которого происходит, когда по всем объектам будет надёжно зафиксировано прохождение экстремума с учётом априорно заданной точности. Второй цикл имеет предопределённое количество итераций (равное количеству вторичных норм, полученных в процессе первого цикла из расчёта на один объект) и включает простой перебор вторичных норм, определение их отклонений от нижней границы переменного доверительного интервала и фиксацию лучшей из всех вторичных норм по каждому объекту.
На заключительном этапе предельного алгоритма осуществляется дополнительное уточнение норм электропотребления, которое производится только для объектов, лучшие вторичные нормы которых выходят за границы переменного доверительного интервала и составляют совокупность так называемых "аномальных норм". Реализация уточняющей процедуры заключается в вычитании (или добавлении) из лучшей вторичной нормы соответствующего его рангу ASR-отклонения, под которым понимается отклонение значения лучшей вторичной нормы от значения нижней или вер-хней границы переменного доверительного интервала (в зависимости от того, где расположена лучшая норма)
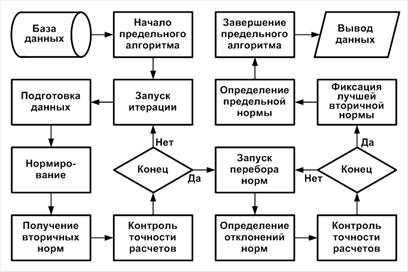
Рис. 10. Схематичный алгоритм одномерной оптимизации.
с учётом коэффициента управляющего воздействия. При этом чем существеннее ASR-отклонение, тем большее значение приобретает коэффициент управляющего воздействия. Следовательно, при реализации вычислительных процедур данного этапа предельного алгоритма от значения лучшей вторичной нормы k-го объекта отнимается (или прибавляется) ASR-отклонение, помноженное на коэффициент управляющего воздействия (рис. 11). В итоге получается предельная норма электропотребления (она же – результирующая ASR-норма из (6)) для k-го объекта техноценоза с учётом лучшей вторичной нормы, ASR-отклонения и коэффициента управляющего воздействия:
|
|
(19) |
где ![]() –
результирующая норма электропотребления, полученная для k-го объекта
техноценоза;
–
результирующая норма электропотребления, полученная для k-го объекта
техноценоза; ![]() – предельная норма k-го объекта;
– предельная норма k-го объекта; ![]() – лучшая вторичная норма, полученная по результатам
оптимизационного процесса;
– лучшая вторичная норма, полученная по результатам
оптимизационного процесса; ![]() – ASR-отклонение,
рассчитанное для k-го объекта;
– ASR-отклонение,
рассчитанное для k-го объекта; ![]() – коэффициент управляющего воздействия k-го объекта.
– коэффициент управляющего воздействия k-го объекта.
В выражении (19) знак "–" ставят в том случае, если точка находится выше верхней границы переменного доверительного интервала, а "+" – если ниже нижней границы. Кроме того, ASR-отклонение определяется в зависимости от положения самóй точки относительно границ переменного доверительного интервала следующим образом:
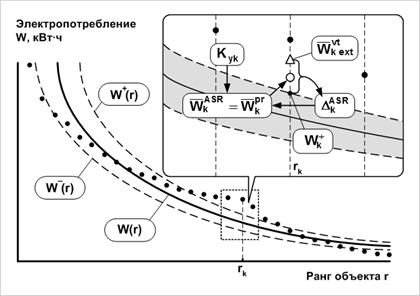
Рис. 11. Получение результирующей (предельной) нормы.
• для объектов, лучшая вторичная норма которых оказалась выше верхней границы переменного доверительного интервала:
|
|
(20) |
• для объектов, лучшая вторичная норма которых лежит ниже нижней границы переменного доверительного интервала:
|
|
(21) |
При определении коэффициента управляющего воздействия может быть реализована различная "политика энергосбережения", также учтены следующие факторы: стохастичность процесса электропотребления; сильная зависимость от метеоусловий; степень мотивации персонала к осуществлению энергосберегающих процедур; возможные существенные изменения технологии потребления электроэнергии; влияние на процесс энергосбережения государственной тарифной политики; вероятная многовариантность структурных изменений в техноценозе и некоторые другие. Мы предлагаем, как минимум, поставить коэффициент управляющего воздействия в прямую зависимость от величины ASR-отклонения. При этом он приобретает смысл линейного весового коэффициента, полученного отдельно на каждом из двух подмножеств аномальных норм:
|
|
(22) |
где ![]() – коэффициент
управляющего воздействия, определяемый для i-й аномальной
нормы;
– коэффициент
управляющего воздействия, определяемый для i-й аномальной
нормы; ![]() – ASR-отклонение для i-й аномальной
нормы; h – общее
количество аномальных норм в подмножестве; j – вспомогательный формальный индекс суммирования.
– ASR-отклонение для i-й аномальной
нормы; h – общее
количество аномальных норм в подмножестве; j – вспомогательный формальный индекс суммирования.
Напомним, что выражение (22) отдельно реализуется для двух групп аномальных норм: 1 – расположенных выше верхней границы доверительного интервала; 2 – расположенных ниже нижней границы. И последнее: для всех лучших вторичных норм, оказавшихся в пределах доверительного интервала, в рамках универсальной вычислительной процедуры можно принять коэффициент управляющего воздействия равным нулю.
Предельный алгоритм нормирования на эмпирическом материале всей имеющейся базы техноценоза позволяет закрепить за каждым объектом на каждом временнóм интервале (час, сутки, месяц, год) индивидуальную норму электропотребления. Процедура аппроксимации даёт динамическую функцию нормы k-го объекта во времени:
|
|
(23) |
где t – время функционирования техноценоза.
Реализация процедур прогнозирования применительно к функции (23) позволяет оценить динамику норм электропотребления объектов, а также разработать программу нормирования техноценоза на среднесрочную перспективу, реализующую, например, следующий критерий:
|
|
(24) |
где n – количество
объектов техноценоза; ![]() –
временнóй диапазон моделирования;
–
временнóй диапазон моделирования; ![]() – кумулятивное требование внешней системы управления
к электропотреблению техноценоза.
– кумулятивное требование внешней системы управления
к электропотреблению техноценоза.
Следует также отметить, что получаемые таким образом нормы эффективны только для исследуемого техноценоза и неприменимы для других, однако для данного техноценоза они надёжны и устойчивы [13, 14]. В любом случае их можно непрерывно (помесячно, ежегодно) уточнять одновременно с изменением базы данных по электропотреблению.
Таким образом, предельный алгоритм нормирования, реализуя один из вариантов ASR-анализа, позволяет определить научно обоснованные нормы электропотребления для каждого объекта техноценоза. Сравнение их с фактическими расходами электроэнергии позволяет всесторонне оценивать энергоэффективность применяемых технологий, своевременно планировать мероприятия и стимулировать работу по энергосбережению, а также обосновывать замену старых технологий на новые.
Литература
1. Указ Президента РФ от 4 июня 2008 года № 889 "О некоторых мерах по повышению энергетической и экологической эффективности российской экономики". – http://www.rg.ru/2008/06/07/ukaz-dok.html.
2. Айвазян С. А., Бухштабер В. М., Енюров И. С., Мешалкин Л. Д. Прикладная статистика: классификация и снижение размерности: справочное издание. М.: Финансы и статистика, 1989. 607 с.
3. Вагин Г. Я. К вопросу о нормировании топливно-энергетических ресурсов на промышленных предприятиях // Промышленная энергетика. 2007. № 3. С. 27–31.
4. Гмурман В. Е. Теория вероятностей и математическая статистика: учебное пособие для вузов. Изд. 7-е, стер. – М.: Высш. шк., 2004. 479 с.
5. Гнатюк В. И. Моделирование и оптимизация в электроснабжении войск: монография. Вып. 4. "Ценологические исследования"". М.: Центр системных исследований, 1997. 216 с.
6. Гнатюк В. И. Оптимальное построение техноценозов. Теория и практика: монография. Вып. 9. "Ценологические исследования". М.: Центр системных исследований, 1999. 272 с.
7. Гнатюк В. И. Закон оптимального построения техноценозов: монография. Вып. 29. "Ценологические исследования". М.: Изд-во ТГУ – Центр системных исследований, 2005. 384 с.
8. Гнатюк В. И. Оптимальное управление электропотреблением регионального электротехнического комплекса (техноценоза): монография. М.: Изд-во ИНП РАН, 2006. 147 с.
9. Гнатюк В. И., Двойрис Л. И. и др. Моделирование систем: учебник. Калининград: Изд-во КПИ, 2009. 650 с.
10. Гнатюк В. И., Луценко Д. В. Прогнозирование электропотребления регионального электротехнического комплекса на инерционном этапе развития: монография. М.: Изд-во ИНП РАН, 2009. 92 с.
11. Гнатюк В. И., Луценко Д. В. Прогнозирование электропотребления на основе GZ-анализа: монография. Калининград: КПИ, 2010. 144 с.
12. Гнатюк В. И. Техника, техносфера, энергосбережение: интернетсайт. – М.: КИЦ "Техноценоз", 2000 – 2011. – http://www.gnatukvi.ru.
13. Гнатюк В. И. Закон оптимального построения техноценозов: компьютерная монография. М.: Изд-во ТГУ – Центр системных исследований, 2005, 2011. – http://gnatukvi.ru/ind.html.
14. Кудрин Б. И. Введение в технетику.2-е изд. Томск: Изд-во ТГУ, 1993. 552 с.
15. Кудрин Б. И. Электроснабжение промышленных предприятий: учебник для ВУЗов. М.: Интермет инжиниринг, 2005. 672 с.
16. Мандель И. Д. Кластерный анализ. М.: Издательство Финансы и статистика, 1988. 76 с.