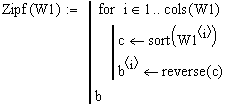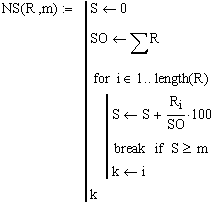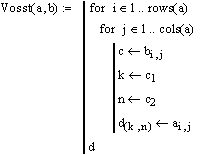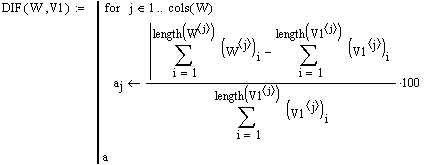// Электрика. – 2007. – № 11.– С. 28–32.

Обработка ранговой параметрической поверхности методом «Singular Spectrum Analysis»

(Опыт применения пакета Mathcad-2001)

В.И. Гнатюк, Д.В. Луценко

Калининградский технический университет

Для эффективного управления ресурсопотреблением техноценоза [1] и реализации тонких процедур рангового анализа (дифлекс-, GZ- и ASR-анализ), подробно описанных в [2], зачастую возникает необходимость исследования его ранговой параметрической поверхности, которая представляет собой двумерное поле рангового параметрического распределения во времени. Очевидно, что на техноценоз в процессе функционирования оказывают влияние несистематические, случайные факторы, искажающие форму ранговой поверхности. Такие искажения могут в значительной степени снизить достоверность тонких процедур рангового анализа. Процедура выделения и устранения несистематических компонент осуществляется при помощи метода Singular Spectrum Analysis (SSA) [3], обладающего простотой и наглядностью. Алгоритм метода SSA для двумерного поля состоит из следующих шагов: преобразования исходной матрицы данных с помощью сдвиговой процедуры в траекторную матрицу; дальнейшего её исследования с помощью анализа главных компонент; восстановления исходной матрицы по выбранным главным компонентам [3, 4]. В конечном итоге, результатом применения метода является разложение матрицы (двумерного поля) на составляющие: систематические (определяемые закономерностью развития процесса во времени) и несистематические ("шум") с последующим удалением "шумовой" составляющей.

Для рангового анализа электропотребления объектов техноценоза [2] использованы данные (за 10 лет) по электропотреблению реально существующего в Калининградской области техноценоза, состоящего из рассредоточенных по всей территории региона 69 объектов (подробно см. [2]). Предварительная процедура подготовки данных и верификации описана ранее*.

Основные понятия

Ранговый анализ – метод исследования больших технических систем (техноценозов), имеющий целью их статистический анализ, а также оптимизацию, и полагающий в качестве основного критерия форму видовых и ранговых распределений. Включает стандартные процедуры интервального оценивания, прогнозирования и нормирования. Более тонкий анализ рангового параметрического распределения позволяет существенно повысить эффективность рангового анализа. Он осуществляется в рамках следующих (так называемых "тонких") процедур: дифлекс-анализа (на этапе интервального оценивания), GZ-анализа (на этапе прогнозирования) и ASR-анализа (на этапе нормирования).

Техноценоз – ограниченная в пространстве и времени взаимосвязанная совокупность далее неделимых технических изделий-особей, объединённых слабыми связями. Связи в техноценозе носят особый характер, определяемый конструктивной, а зачастую и технологической независимостью отдельных технических изделий и многообразием решаемых задач. Взаимосвязанность техноценоза определяется единством конечной цели, достигаемой с помощью общих систем управления, обеспечения и др. Оптимальное управление техноценозом является особой процедурой и реализуется посредством ТЦ-оптимизации.

1. Подготовка данных. С целью упорядочения индексации в матрицах и векторах, используемых в программе, зададим начало отсчёта:

Далее импортируем данные по электропотреблению для последующей обработки. При этом программными средствами числовые значения из файла "c:\mathcad_dat\data_d.xls" присваиваются соответствующим элементам матрицы V [5]:

При необходимости можно осуществить просмотр данных непосредственно в теле программы:

Построим табулированные ранговые параметрические распределения техноценоза по электропотреблению:

Таким образом, столбец матрицы V1 представляет собой ранговое параметрическое распределение исследуемого техноценоза на определённом временнóм интервале (год). Визуализируем данные (рис. 1):

Здесь рис. 1

2. Преобразование матрицы данных с помощью сдвиговой процедуры в траекторную матрицу. Преобразование матрицы ранговых параметрических распределений при помощи матрицы-окна определённого размера в траекторную матрицу подробно описано в работах [3, 4]. Подпрограмма GS(a) предназначена для преобразования матрицы-окна в вектор:

Чтобы в дальнейшем можно было восстановить исходную матрицу, создадим специальную матрицу индексов. При этом матрица индексов должна совпадать по размеру с исходной матрицей ранговых параметрических распределений:

Зададим размер матрицы-окна:

Далее преобразуем матрицу ранговых параметрических распределений и матрицу индексов по алгоритму, описанному в [3]:

3. Исследование траекторной матрицы с помощью анализа главных компонент. В первую очередь найдём ковариационную матрицу:

Далее найдём собственные числа ковариационной матрицы [4, 5] и визуализируем их (рис. 2):


Определим количество собственных чисел, объясняющих заданную долю дисперсии [4]: _:

Таким образом, для нашего примера количество собственных чисел, объясняющих 98,89 % дисперсии, составляет:

Найдём собственные вектора по определённому выше количеству собственных чисел. Процедуру их нахождения можно рассматривать как задание нового многомерного базиса, на направлениях орт которого дисперсия максимальна [3, 4]:

Найдём главные компоненты. При этом осуществляется проецирование ("натягивание") исходной многомерной совокупности данных на орты в пространстве меньшей размерности [3, 4]:

4. Восстановление исходной матрицы по выбранным главным компонентам. Восстановим траекторные матрицы соответственно по первой, второй и третьей главным компонентам [3, 4]:

Восстановим матрицу ранговых параметрических распределений:

В результате проделанных процедур получаем разложение матрицы ранговых параметрических распределений (рис. 2, 3):

Первая главная компонента является основной в разложении. Она задаёт структуру ранговой параметрической поверхности техноценоза по электропотреблению и описывает техноценоз в целом. В известном смысле её можно считать "ципфовой компонентой". Вторая главная компонента является вторичной (с точки зрения порядка величин). Она задаёт тренд процесса электропотребления и имеет отношение, в основном, к ноевой и пойнтер-кастам техноценоза, её можно считать "гауссовой компонентой разложения". Третья главная компонента является третичной (с точки зрения порядка величин). Она задаёт цикличность процесса электропотребления и имеет отношение, в основном, к ноевой и старшим пойнтер-кастам техноценоза. Её также можно считать "гауссовой компонентой разложения" [2]. Очевидно, что для нахождения результирующей матрицы необходимо сложить отдельные компоненты (рис. 4):

Проанализируем отклонения восстановленных значений (матрица W, рис. 4) от исходных эмпирических (см. матрица V1, рис. 1) [2]:

Таким образом, в ходе реализации программы удалось разложить матрицу ранговых параметрических распределений, определить её главные компоненты, а также восстановить данные после удаления несистематических составляющих. При этом суммарное максимальное относительное отклонение восстановленных значений от исходных эмпирических на одном временнóм интервале не превысило 5 %. Следовательно, задача удаления "шумовой" составляющей решена без потери полезной информации.

Список литературы

1. Кудрин Б. И. Введение в технетику. Томск: Изд-во ТГУ, 1993. 552 с.

2. Гнатюк В. И. Закон оптимального построения техноценозов. М.: Изд-во ТГУ – Центр системных исследований, 2005. 384 с. (http://www.baltnet.ru/~gnatukvi/ind.html).

3. Данилов Д. Л., Жиглявский А. А. Главные компоненты временных рядов: Метод "Гусеница". СПб.: СПбГУ, 1997. 308 с. (http://www.gistatgroup.com/gus).

4. Айвазян С. А., Бухштабер В. М., Енюков И. С., Мешалкин Л. Д. Прикладная статистика: Классификация и снижение размерности. М.: Финансы и статистика, 1989. 607 с.

5. Дьяконов В. П. MATHCAD 8/2000: Специальный справочник. СПб.: Питер, 2001. 592 с.

Рис. 1. Трёхмерная ранговая параметрическая поверхность техноценоза:

V1 – исходная эмпирическая матрица данных; абсцисса – ранг объекта; ордината – временной интервал (год); аппликата – электропотребление, кВтч.

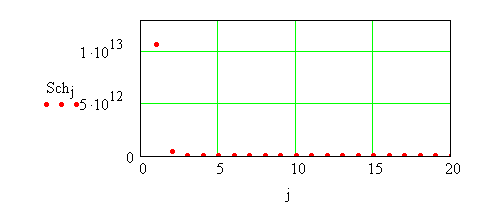
Рис. 2. Собственные числа ковариационной матрицы:

абсцисса – порядковый номер числа; ордината – значение собственного числа.

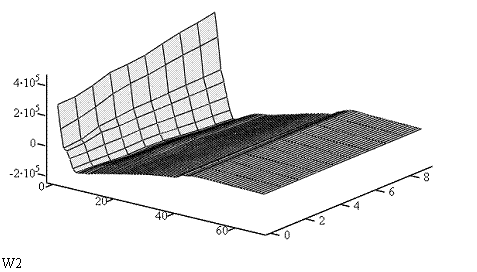
Рис. 3. Трёхмерные ранговые поверхности техноценоза, восстановленные по главным компонентам: а, б, в – соответствуют матрицам W1, W2 и W3 –соответственно первой, второй и третьей главных компонент; абсцисса – ранг объекта; ордината – временные интервалы (годы); аппликата – электропотребление (знак учитывает отклонения второй и третьей компонент), кВтч.

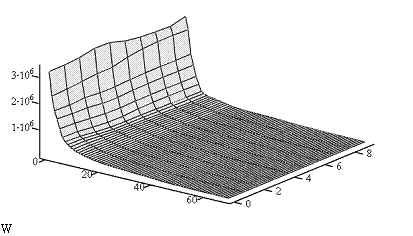
Рис. 4. Трёхмерная ранговая поверхность техноценоза, восстановленная по трём главным компонентам: W – восстановленная матрица данных; абсцисса – ранг объекта; ордината – временные интервалы (годы); аппликата – электропотребление, кВтч.